- 東京大学教養学部統計学教室
- 東京大学出版会
機械学習勉強会として今は統計学入門をやっている。 週一でやっていて、今週から輪読形式で進めてみることになった。
また、勉強会で書いたコードや疑問点などをまとめるためにGitHubのレポジトリを活用している。 https://github.com/Wondershake/ml-statistics-intro
今回の内容
第6章 確率分布
様々な現象にあてはまる確率分布を紹介する。
6.1 超幾何分布
- 超幾何分布 (hypergeometric distribution)
- Aが$M$個、Bが$N-M$個の2種類からなる$N$個の集団があるとき
- この集団から$n$個取り出したときにAが$x$個、Bが$n-x$個であるとする
- $f(x)=\frac{{}MC_x\cdot{}{N-M}C_{n-x}}{{}_NC_n}$
- $x=\max(0, n-(N-M)),\dots, \min(n, M)$
- 確率変数$X$が超幾何分布に従うとき、
- 期待値: $E(X)=n\frac{M}{N}$
- 分散: $V(X)=n\frac{M(N-M)}{N^x}\frac{N-n}{N-1}$
- $N$が無限に大きければ$V(X)\rightarrow1$
- 捕獲再捕獲法 (capture-recapture method)
- 資源調査に使われる
- $N:M=n:x$が成立するとき$f(x)$が最大になる性質を利用して未知の$N$を推定する
- 非復元 (without replacement): $x$個のものを取り出すとき、1個ずつ元に戻さずに取り出す
- 復元 (with replacement): 1個ずつ元に戻す
- 超幾何分布は非復元の場合
- 復元の場合は$\frac{M}{N}=p$とした二項分布に従う
6.2 二項分布とベルヌーイ分布
- ベルヌーイ試行 (Bernoulli trials)
- 2種類の可能な結果(成功、失敗)を生じる実験があり、それぞれの確率を$p, 1-p$とする
- この実験を同じ条件かつ独立に$n$回繰り返す試行のことをベルヌーイ試行という
- 二項分布 (binomial distribution)
- ベルヌーイ試行で成功が$x$回、失敗が$n-x$回生じるとする
- その確率は$f(x)={}_nC_xp^x(1-p)^{n-x}$
- $x=0, 1, \dots, n$
- $Bi(n, p)$で表す
- $Bi(1, p)$を**ベルヌーイ分布 (Bernoulli distribution)**という
- 期待値: $E(X)=np$
- 分散: $V(X)=np(1-p)$
6.3 ポアソン分布
- ポアソンの小数の法則 (Poisson’s law of small numbers)
- 二項分布において$n$が大きく$p$が小さい場合
- $np\rightarrow\lambda$となるように$n\rightarrow\infty, p\rightarrow0$となる極限で
- ${}_nC_xp^x(1-p)^{n-x}\rightarrow \frac{e^{-\lambda}\lambda^x}{x!}$
- ポアソン分布 (Poisson distribution)
- $\lambda>0$として
- $f(x)=\frac{e^{-\lambda}\lambda^x}{x!}$
- $x=0, 1, 2, \dots$
- $P_o(\lambda)$で表す
- 期待値: $E(X)=\lambda$
- 分散: $V(X)=\lambda$
6.4 幾何分布と負の二項分布
- 幾何分布 (geometric distribution)
- ベルヌーイ試行と同じ問題で
- 試行回数を決めないで最初に成功が得られるまでの回数を$x$とする
- $q=1-p$とする
- $f(x)=pq^{x-1}$
- $x=1, 2, \dots$
- 期待値: $E(X)=\frac{1}{p}$
- 分散: $V(X)=\frac{1-p}{p^2}$
- 離散的な**待ち時間分布 (waiting time distribution)**と呼ばれる
- 負の二項分布 (negative binomial distribution)
- 幾何分布の一般化
- $k$回目の成功を得るまでの失敗の回数を$x$とする
- $f(x)={}_{k+x-1}C_xp^kq^x$
- パスカル分布ともいう
- $k=1$のとき幾何分布
- 期待値: $E(X)=\frac{kq}{p}$
- 分散: $V(X)=\frac{kq}{p^2}$
6.5 一様分布
- 離散一様分布 (uniform distribution of descrete type)
- $N$面さいころを振ったときに出る目を$X$
- $f(x)=\frac{1}{N}$
- $x=1,2,\dots,N$
- 期待値: $E(X)=\frac{N+1}{2}$
- 分散: $V(X)=\frac{N^2-1}{12}$
6.6 正規分布
- 正規分布 (normal distribution)
- 非常に重要な連続型の確率分布
- 例えば測定誤差は正規分布に従って生じるとされている
- **ガウス分布 (Gaussian distribution)**とも
- $f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\frac{-(x-\mu)^2}{2\sigma^2}$
- $-\infty<x<\infty$
- $E(X)=\mu$
- $V(X)=\sigma^2$
- ${\rm N}(\mu,\sigma)$で表す
- 著しい特徴
- $X$が$N(\mu,\sigma^2)$に従っているとき、$Y=aX+b$は$N(a\mu+b,a^2\sigma^2)$に従う
- 標準化変数$Z=\frac{X-\mu}{\sigma}$は$N(0,1)$に従う。これを**標準正規分布 (standard normal distribution)**という
- 非常に重要な連続型の確率分布
- 中心極限定理 (central limit theorem)
- 同一の確率分布$f(x)$をもつ$n$個の独立な確率変数の和$X_1+X_2+\dots+X_n$は$n$が大きいとき正規分布に従っていると仮定してよい
6.7 指数分布
- 指数分布 (exponential distribution)
- $x\geq0$のとき$f(x)=\lambda e^{-\lambda x}$
- $x<0$のとき$f(x)=0$
- 本書では$Ex(\lambda)$
- $x\geq0$のとき$F(x)=P(X\leq x)=1-e^{-\lambda x}$
- $x<0$のとき$F(x)=0$
- 待ち時間分布の性質を持つ
- $E(X)=\frac{1}{\lambda}$
- $V(X)=\frac{1}{\lambda^2}$
- $P(X>x)=e^{-\lambda x}; (x\geq0), 1;(x<0)$
6.8 ガンマ分布
- ガンマ分布 (Gamma distribution)
- 指数分布の一般形
- $x\geq0$のとき$f(x)=\frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}$
- $x<0$のとき$f(x)=0$
- $\Gamma(\alpha)=\int_0^\infty x^{\alpha-1}e^{-x}dx$
- $E(X)=\frac{\alpha}{\lambda}$
- $V(X)=\frac{\alpha}{\lambda^2}$
- $Ga(\alpha,\lambda)$で表す
- $Ga(1, \lambda)=Ex(\lambda)$
- 確率変数$X_1,X_2,\dots,X_\alpha$が独立で$Ex(\lambda)$に従うとき、$X_1+X_2+\dots+X_\alpha$は$Ga(\alpha,\lambda)$に従う
- 確率変数$X$が${\rm N}(0,1)$に従うとき、$X^2$は$Ga(\frac{1}{2},\frac{1}{2})$に従う
- $\chi^2$(カイ二乗)分布: $Ga(\frac{n}{2}, \frac{1}{2})$を自由度$n$の$\chi^2$分布という
6.9 ベータ分布と一様分布
- ベータ分布 (Beta distribution)
- $0<x<1$のとき$f(x)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$
- それ以外では$f(x)=0$
- ただし、$\alpha>0, \beta>0$
- $B(\alpha,\beta)=\int_0^1x^{\alpha-1}(1-x)^{\beta-1}dx=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$
- $E(X)=\frac{\alpha}{\alpha+\beta}$
- $V(X)=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$
- $Be(\alpha, \beta)$で表す
- $\alpha=\beta=1$のとき一様分布
6.10 コーシー分布
- コーシー分布 (Cauchy distribution)
- $f(x)=\frac{\alpha}{\pi\{\alpha^2+(x-\lambda)^2\}} ; (\alpha>0)$
- 期待値、分散、モーメント母関数が存在しない
6.11 対数正規分布
- 対数正規分布 (log-normal distribution)
- $x>0$のとき$f(x)=\frac{1}{\sqrt{2\pi}\sigma x}\exp(-\frac{(\ln(x)-\mu)^2}{2\sigma^2})$
- $x\leq0$のとき$f(x)=0$
- $\ln X$が正規分布に従うとき、$X$は対数正規分布に従う
- $E(X)=\exp(\mu+\frac{\sigma^2}{2})$
- $V(X)=\exp(2\mu+2\sigma^2)-\exp(2\mu+\sigma^2)$
- 所得分布で有名
6.12 パレート分布
- パレート分布 (Pareto distribution)
- $x\geq x_0$のとき$f(x)=\frac{a}{x_0}(\frac{x_0}{x})^{a+1}$
- $x<x_0$のとき$0$
- $E(X)=\frac{ax_0}{a-1};(a>1)$
- $V(X)=\frac{ax_0^2}{a-2}-(\frac{ax_0}{a-1})^2;(a>2)$
- 高額所得者の所得分布
- $x_0$以上の所得の確率
6.13 ワイブル分布
- ワイブル分布 (Weibul distribution)
- センター試験の得点分布
練習問題
https://github.com/Wondershake/ml-statistics-intro/issues/12
正解かどうかはわからん 😅
6.1
教科書(p.130)にまるまる載ってる
6.2

6.3

6.4

6.5

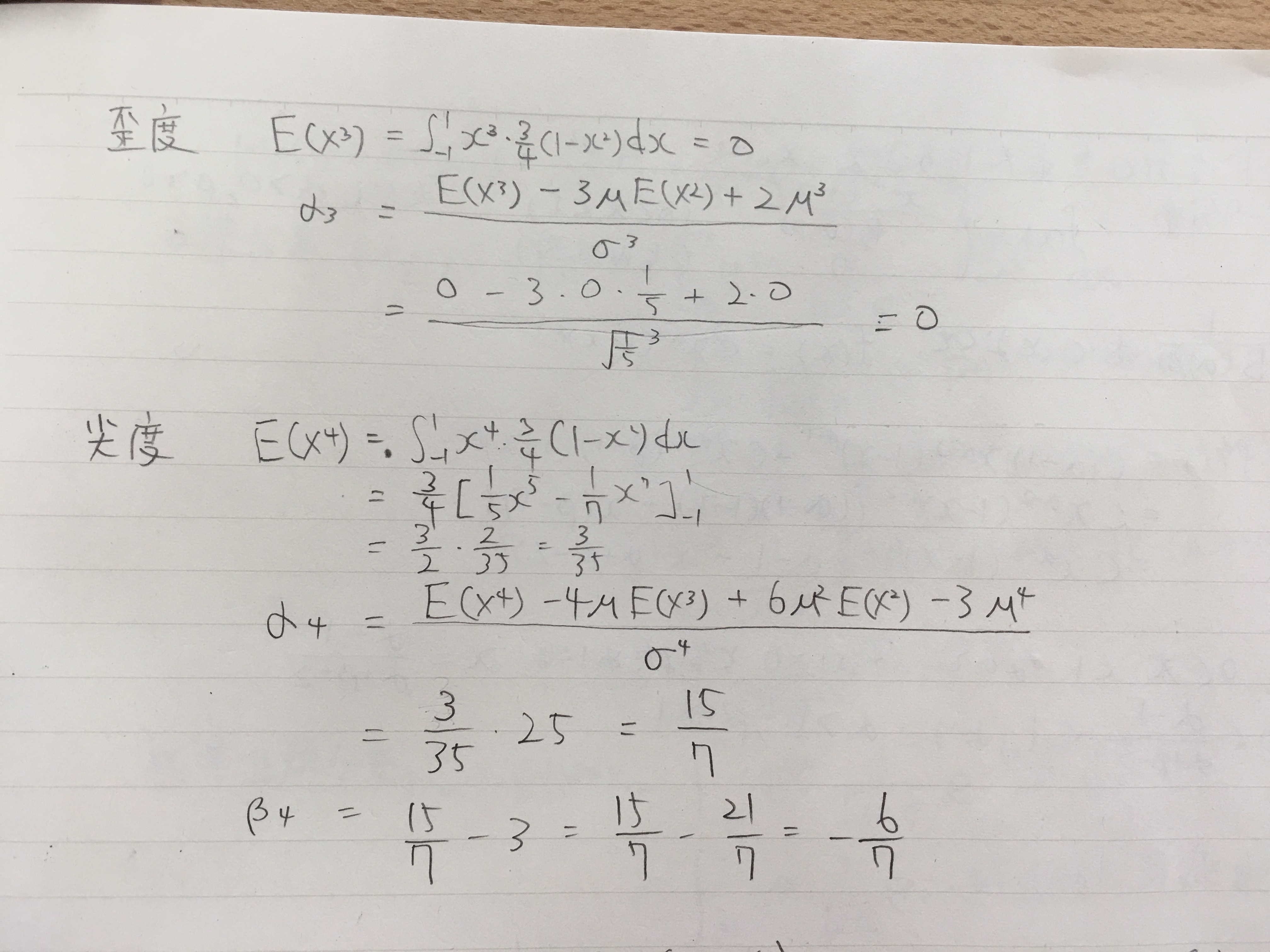
6.6
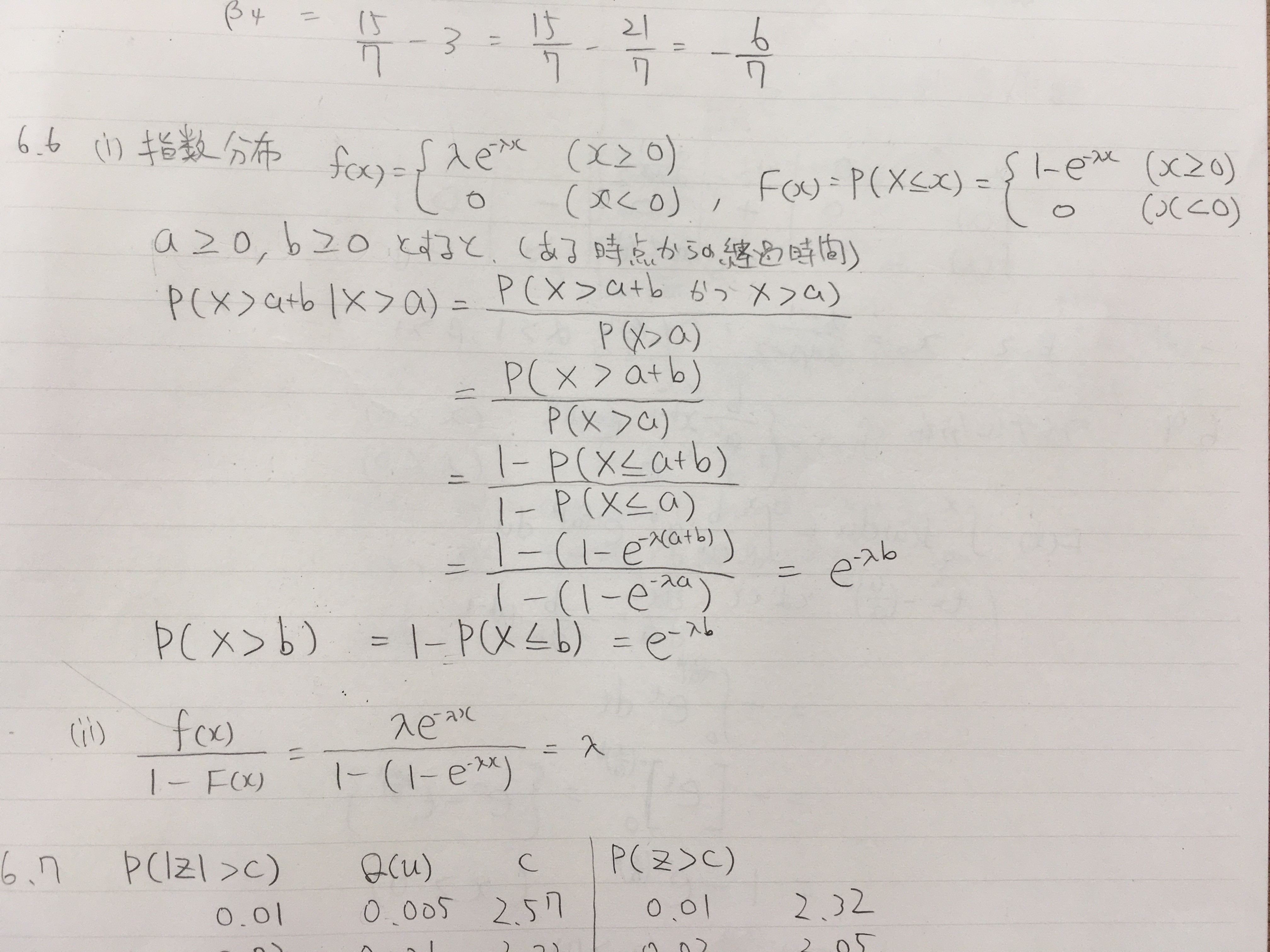
6.7

6.8
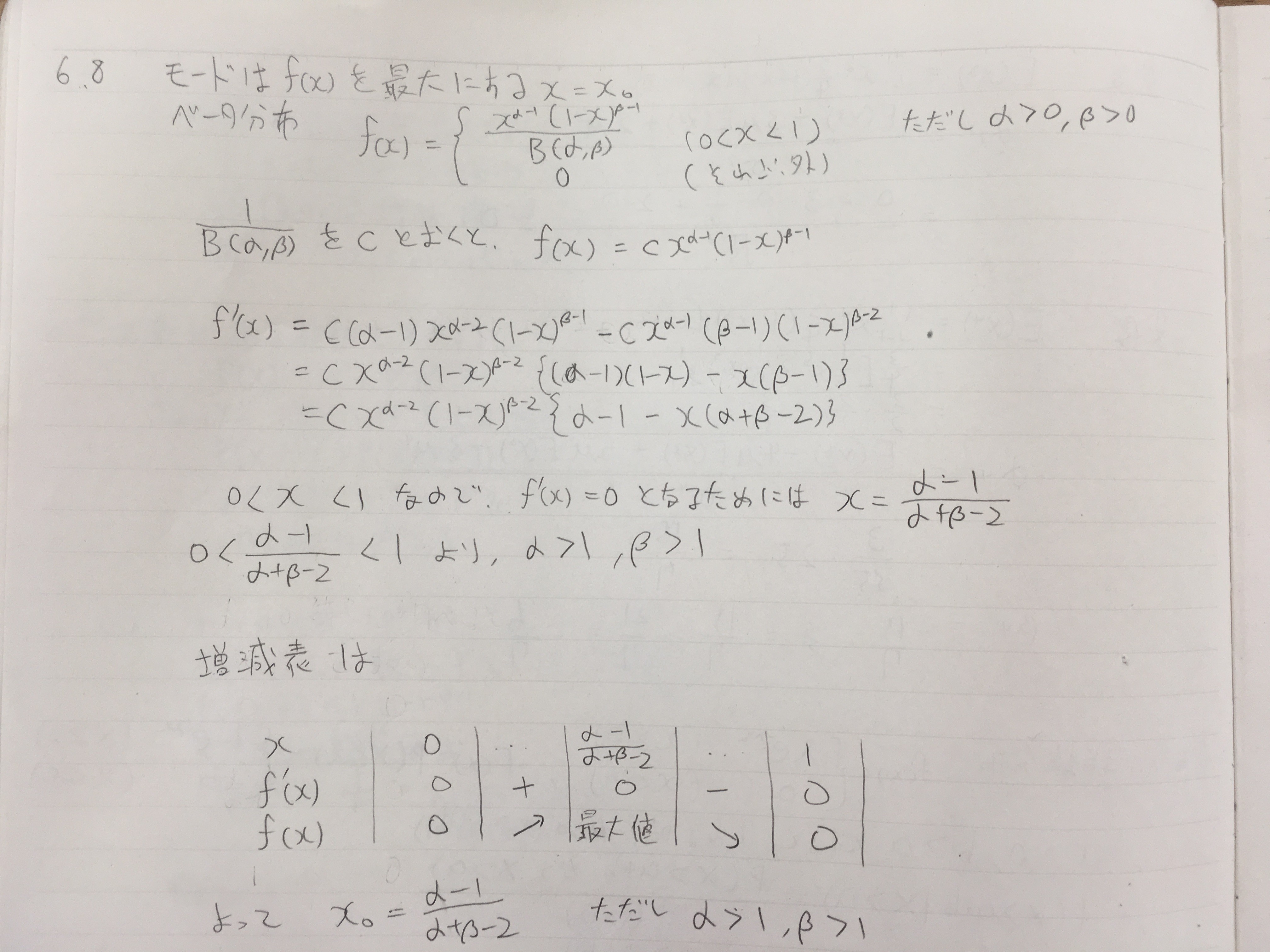
6.9
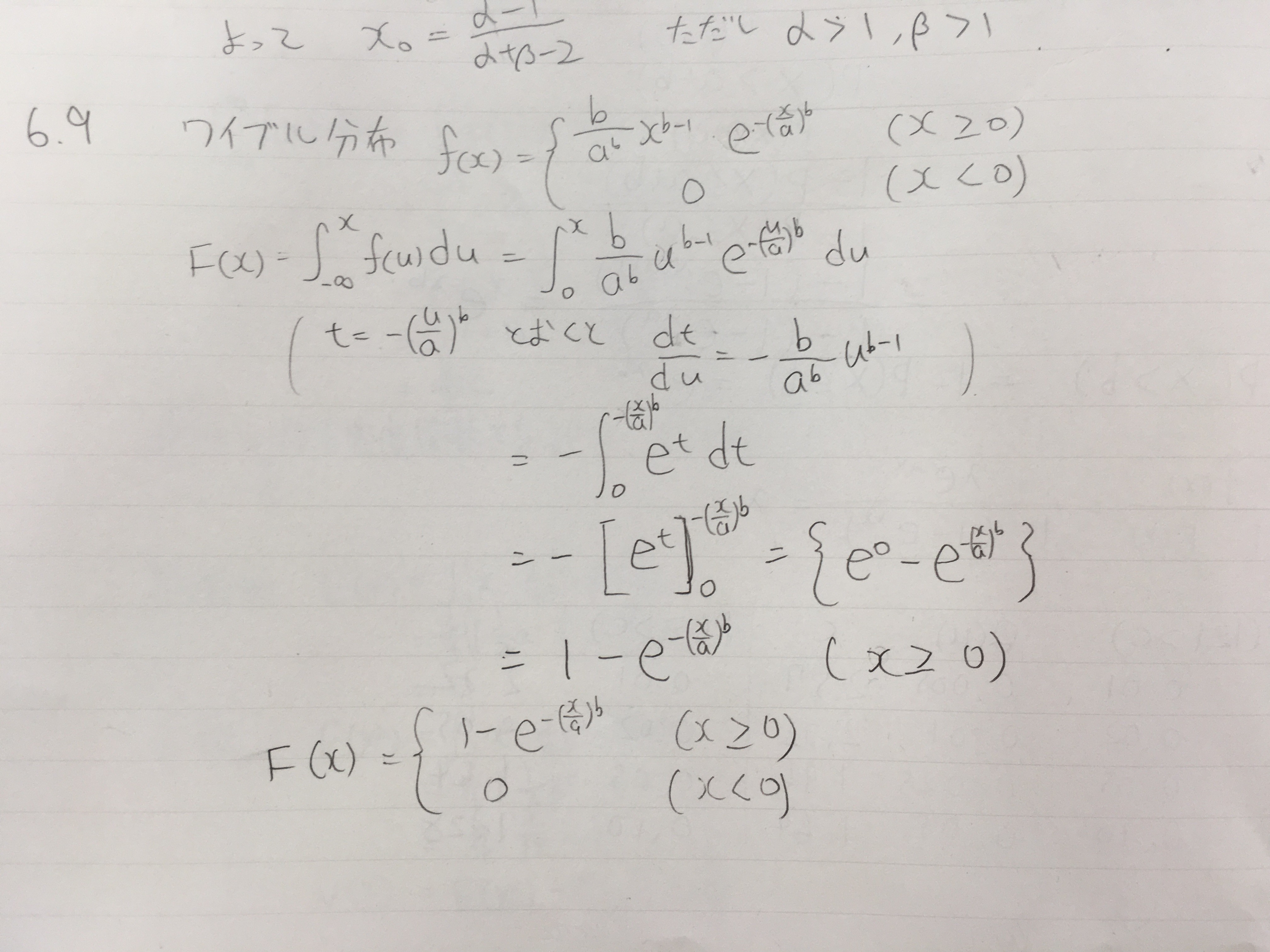
6.10
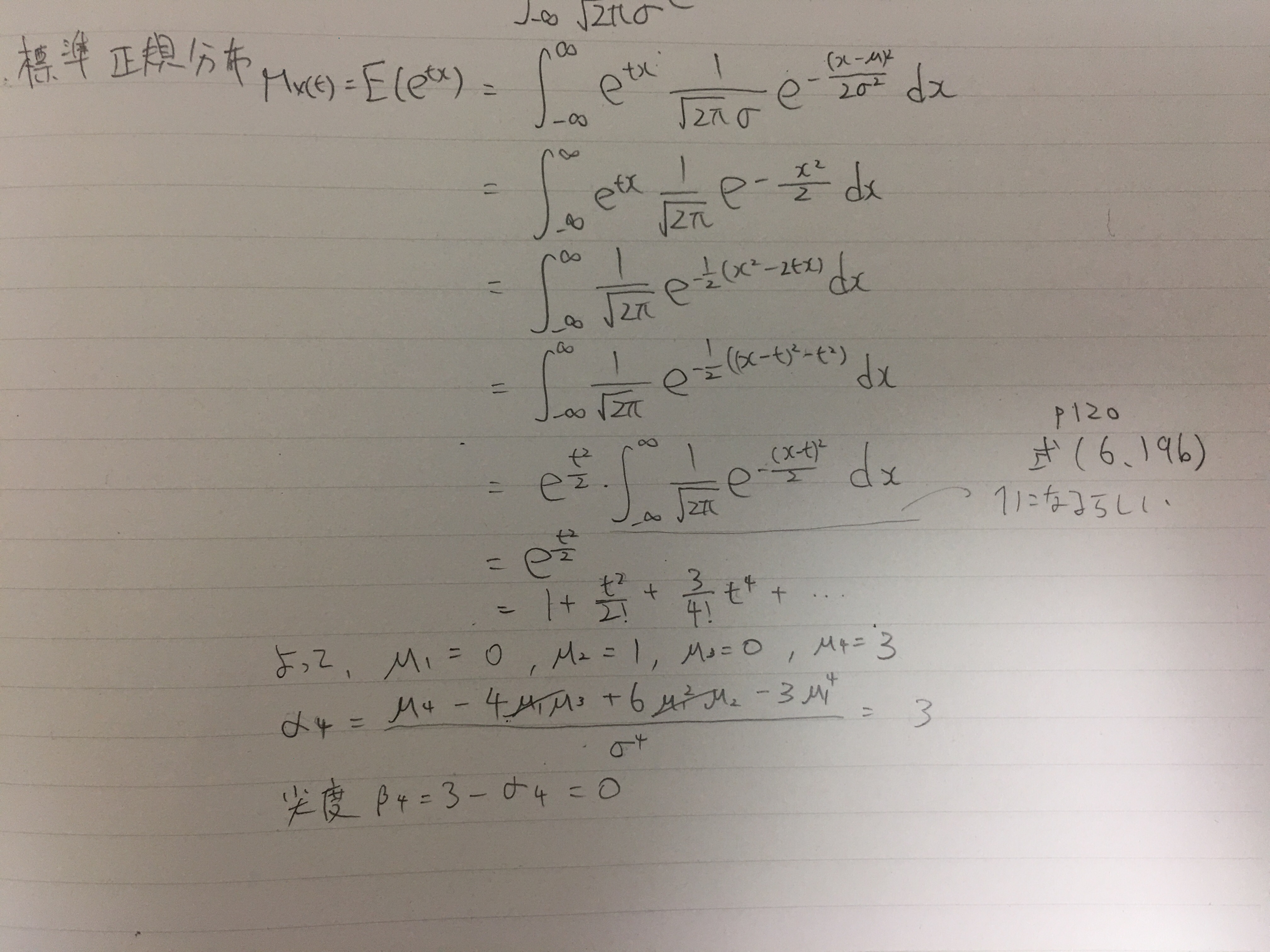
所感
- 輪読形式でやるとまじめに勉強せざるを得ないので良い
- 確率統計にはかなりの苦手意識があったけど、時間をかけてちゃんと勉強すればある程度わかった感が得られているので良い
- 学生時代はできていたはずの微分積分力ができなくて辛い
- 練習問題時間かかって辛い
次回
第7章 多次元の確率分布
